【基本情報】絶対誤差と相対誤差の違いと求め方をわかりやすく解説

この記事で解決できる内容

※タップすると該当箇所までジャンプできます。

こうした悩みをお持ちの方へ向けた記事です。

誤差とは、同じ計算をしているのに、表現の方法で違った数値になってしまうような差のことで、なんとなくで理解している人も多いと思います。

しかし、いざ「絶対誤差を求めなさい」とか「絶対誤差は〇〇」と「絶対」や「相対」を付けられるだけで少し不安になったりしますよね。

そこでこの記事では、基本情報の問題に出てくる「絶対誤差」や「相対誤差」のような「○○誤差」について解説していきます。

基本情報技術者試験を勉強中だったり、○○誤差について違いを知りたい人は最後まで読んでみてください。

>> Udemyで基本情報技術者試験を学習したいならおすすめの講座はこちら！

Udemyで基本情報技術者試験合格を目指す！おすすめ講座5選！

続きを見る

絶対誤差と相対誤差の違いについて

誤差とは真の値（論理的に正しい値）とは差異が出てしまうこと、またはその差異のことを指します。誤差には「絶対誤差」と「相対誤差」があります。

絶対誤差とは、真の値と測定値・演算結果との差のことで、例えば、実際の体重は50kgなのに対して実際に体重計に乗ると51kgだった時、絶対誤差は1kgです。

一方、相対誤差はパーセントで表した誤差のことです。上の例で言うと、(51-50) ÷ 50 × 100 = 2% が相対誤差となります。

なぜ「絶対誤差」と「相対誤差」が必要なのか

絶対誤差だけだと、実際の現場での計算などのときに、「無視していい誤差」なのか「無視してはいけない重大な誤差」なのかを判断できないことがあります。

例えば、先程の重量の誤差でいうと、100Kgの誤差が出ていたとしましょう。「かなり大きい誤差だなぁ」と感じるかと思うのですが、総重量が10トンとかの内で100Kgであれば相対誤差は1％なので、「あれ？大きくもないのか？」となります。

このように、絶対誤差だけだと「大きい誤差なのか」「気にしなくていい誤差なのか」を判断できない場合に相対誤差も必要だよ！ということですね！

例題で分かる「絶対誤差」と「相対誤差」の計算方法

下記の例題では、具体的な絶対誤差と相対誤差の計算方法を紹介していきます。

例題を解くことで誤差の計算のイメージをつかみましょう！

(例題)三つの実数X.Y.Zとそれぞれの近似値が次の場合、相対誤差の小さい順に並べなさい。

	真の値	近似値
X	2.02	2
Y	0.97	1
Z	4.04	4

近似値を使って計算することで生じる誤差の大小を相対誤差を計算して比較する問題です。

近似値とは、近寄った似ている値のことで、例題のように2.02を 2 で計算すること。真の値(2.02)ではなく近似値(2)で計算することで生じる誤差の大小を比較するわけです。

絶対誤差と相対誤差の違いを分かりやすくするために下記のような表を作りました。

	真の値	近似値	絶対誤差	相対誤差
X	2.02	2
Y	0.97	1
Z	4.04	4

絶対誤差の計算方法 ｜ 真の値と測定値・演算結果との差

Xの絶対誤差は ⇒ 2.02 - 2 = 0.02
Yの絶対誤差は ⇒ ｜0.97 - 1 ｜ = 0.03
Zの絶対誤差は ⇒ ｜4.04 - 4｜ = 0.04

	真の値	近似値	絶対誤差	相対誤差
X	2.02	2	0.02
Y	0.97	1	0.03
Z	4.04	4	0.04

絶対誤差だけで見たら、Zが一番大きいですが、相対誤差だと変わってくるのです。

相対誤差の計算方法 ｜ 絶対誤差 ÷ 理論値 × 100 (％)

X：2 ÷ 2.02 × 100 = 0.99001%
Y：0.03 ÷ 0.97 × 100 = 3.09%
Z：0.04 ÷ 4.04 × 100 = 0.990099%

	真の値	近似値	絶対誤差	相対誤差
X	2.02	2	0.02	0.99％
Y	0.97	1	0.03	3.09％
Z	4.04	4	0.04	0.99％

Yは明らかに大きいことがわかりましたが、四捨五入すると、XとZの大小がわからないので、他の方法で大小を比較することにします。

分数を使って比較する

今回の例題では、0.99％とほとんど相対誤差の大小がわからなかったので、分数の性質を使って大小を比較します。具体的には分母か分子を同じにすれば大小関係を比較する事ができます。

3ステップでそれぞれの相対誤差を求めていきます。

① 小数は間違いやすいので、100倍してからまずは絶対誤差を求める。

X = (2.02-2)×100= 2
Y = (|0.97-1|)×100 = 3
Z = (4.04-4)×100 = 4

②Zを4で割る

X = (2.02-2)×100= 2
Y = (|0.97-1|)×100 = 3
Z = (4.04-4)×100 = 4 →(1.01-1)×100 = 1

③分子の絶対誤差を揃えるのが簡単そう！　6で揃える・

絶対誤差を6にする時、X.Y.Zそれぞれの真のは

X = 306
Y = 394
Z = 606

分子が同じであれば、分母が大きいほど数は小さくなるので、相対誤差の大小関係は　Z→Y→X

【基本情報】誤差の種類①：丸め誤差とは？

丸め誤差とは、浮動小数点表示をすることによって出てしまう差異のことです。

例えば、10進数の0.1を、もしも仮数が4ビットの浮動小数点形式であらわすとすると、0.000110011001100110・・・となりきれいに表すことができません。

そのため有効桁が定められる、もしくは浮動小数点表示で表すと下位が切り捨てられて、実際の数字よりも少し小さく見られてしまいます。

このようにビット数が制限されたことによって切り捨てが行われて生じる誤差を丸め誤差と呼びます。

情報処理での誤差の種類②：打ち切り誤差とは？

打ち切り誤差とは、無限小数を途中で打ち切って表現する時の誤差のことです。

例えば、1÷3=0.333333333••• のように割り切れない無限小数をコンピュータで表示する場合を考えてください。

小数点以下の有効桁数が3桁とすると。0.333と表示され、それ以下を打ち切ります。

このように実際の値との差異が生じることを打ち切り誤差と言います。

情報処理での誤差の種類③：情報落ち誤差とは？

情報落ち誤差とは、絶対値の大きな値と絶対値の小さな値の足し算や引き算を行った時、小さい数が計算結果に反映されないために生じる誤差のことです。

例えば、仮数が4ビットの条件付きで 0.1111 ✕ 2⁴ + 0.1111 ✕ 2^-1 を計算してみましょう。

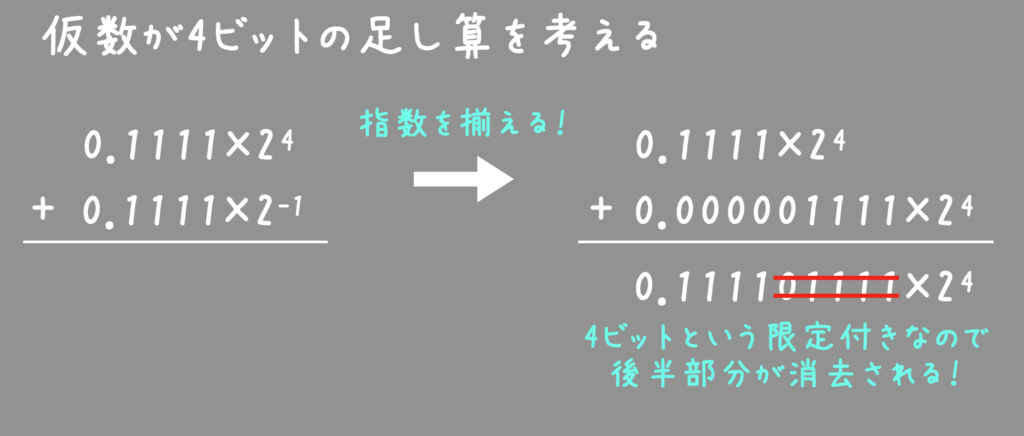
ちゃんと、0.1111 ✕ 2^-1 を足したのにも関わらず、仮数が4ビットの条件があると、計算結果も変わらず、+ 0.1111 ✕ 2^-1 の部分があってもなくても同じ。つまり情報が落ちてしまっています。

このように、絶対値が大小が離れていることで、計算した結果が反映されないことを情報落ち誤差と呼びます。

情報処理での誤差の種類④：桁落ち誤差とは？

桁落ち誤差とは、ほぼ等しい小数の値同士の引き算したあと、正規化することで、生じてしまう差異のことです。

正規化とは、仮数の左側に0が来ないように指数を操作することです。

ほぼ等しい2つの値の差を求めた時にビットが制限されていることによって生じる誤差を桁落ち誤差と呼びます。

まとめ

今回は誤差には種類があること、それぞれの種類の特徴と違いをまとめました。

情報処理において誤差が生じるのは、表示する範囲が限られているために起こります。あとはどのシチュエーションで生じる誤差で名前が変わるだけなのでそこは繰り返し覚えていきましょう。

小中学生で四捨五入を習ったのでそれをイメージした貰えばわかりやすいですね。

基本情報技術者試験の午前試験でしばしば出題される誤差の問題、資格取得しようと思っている方はぜひ頭に入れておきましょう！

もっと基本情報技術者試験を体系的に学び、一発合格を目指しているのであれば、以下の記事で参考書を選ぶか、オンライン講座を利用してみるのがおすすめです！是非チェックしておいてください！

基本情報技術者試験に合格するためのオンライン講座おすすめ3選

続きを見る