【基本情報技術者試験】IEEE形式の浮動小数点表示は何が違うのかわかりやすく解説！

8bitのパソコンで、0.0000000025はどう表現するのでしょうか？

そんなとき便利なのが浮動小数点表示です。

浮動小数点表示は、通常の小数 0.0000000025を 2.5 ✕ 10^-8 と掛け算を使うことで表現する方法です。

つまり浮動小数点表示を使うと、どんな桁数の小数でも、表現することができます。

この2進数で表された基数でも浮動小数点表示を用いる場面が多々ありますので、今回は浮動小数点表示についてわかりやす解説します。

基数で負数を表現する方法からわからない場合はこちらの記事で確認してください！

さらに、2進数の浮動小数点表示には、IEEE形式とIBM方式があり、一般的にはIBM方式が用いられますが、基本情報技術者試験ではIEEE形式も出題されるため、2つの方式について触れていきます。

浮動小数点表示とは？

小数の表示方法には、固定小数点表示と浮動小数点表示の2種類あります。

固定小数点表示では、8ビットで0.0000000125などは表示することができないので、そんなときに登場するのが浮動小数点表示を使うことで小数を表現します。

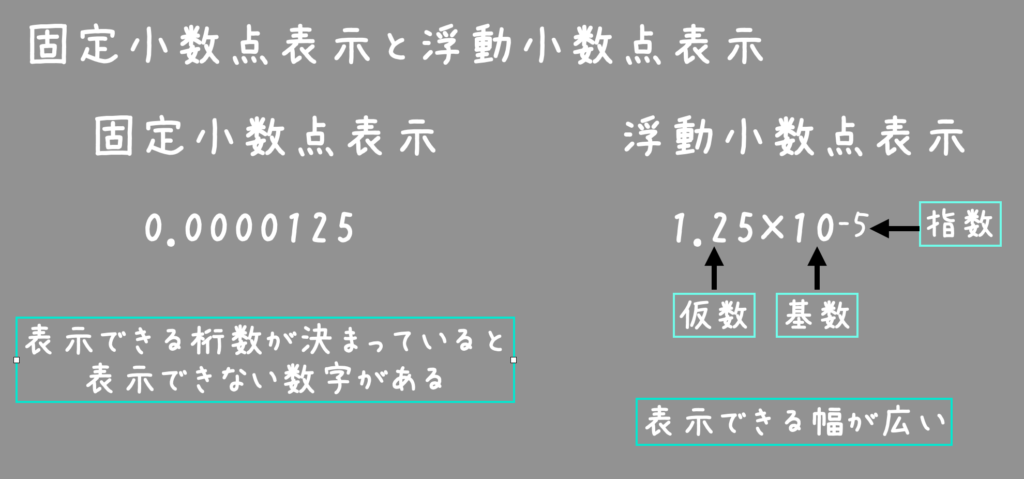
浮動小数点表示をつかうのにはメリットとデメリットがあるので、今回は浮動小数点表示をマスターしていきましょう。

2進数の浮動小数点表示ってどんな感じ？

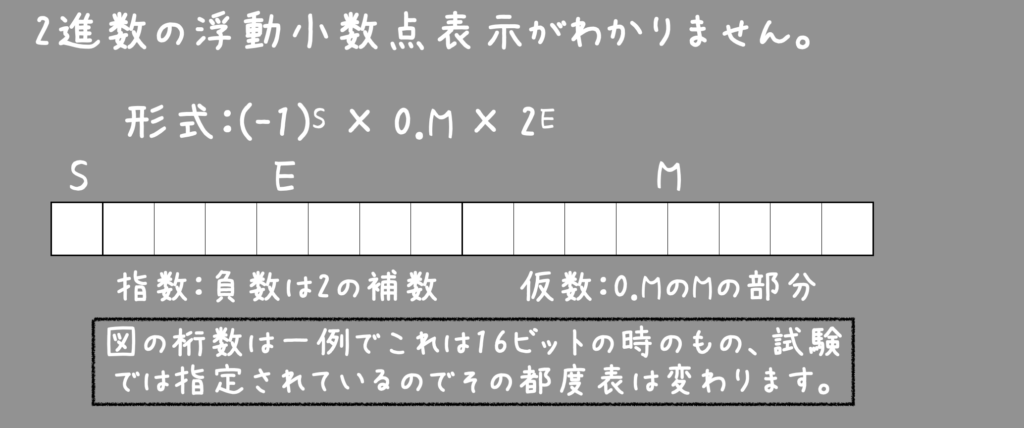
2進数の浮動小数点表示は下図のように (-1)^s×0.M×2^E で表します。

• S・・・符号　(1なら負、0なら正)
• E・・・指数　小数点を何個ずらすか（正なら左へ、負なら右へずらす)
• M・・・仮数　

をそれぞれ表します。

(例)1000101010100000 の16ビットの解読

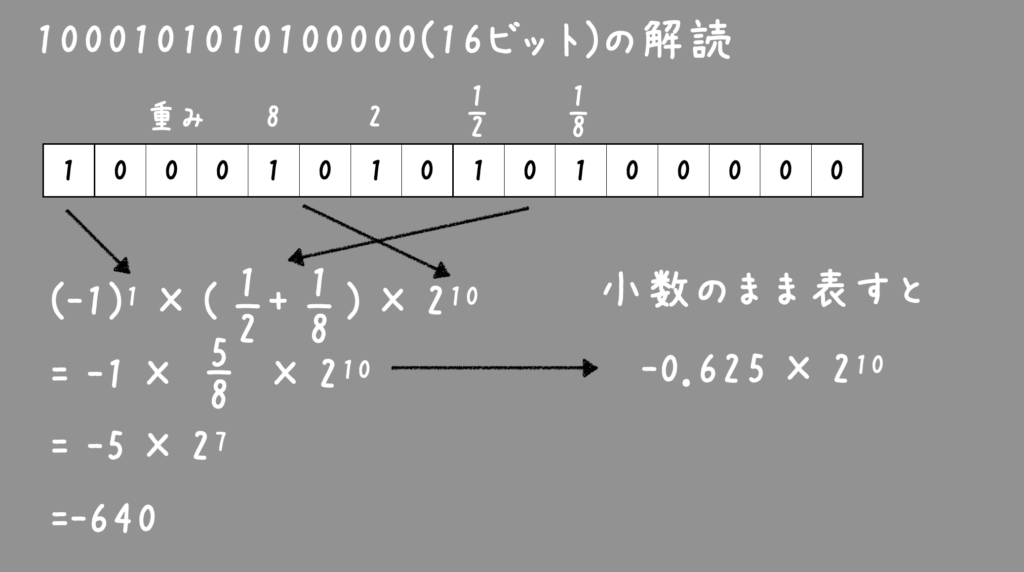
(例)10進数の+37を2進数の浮動小数点表示にしなさい。

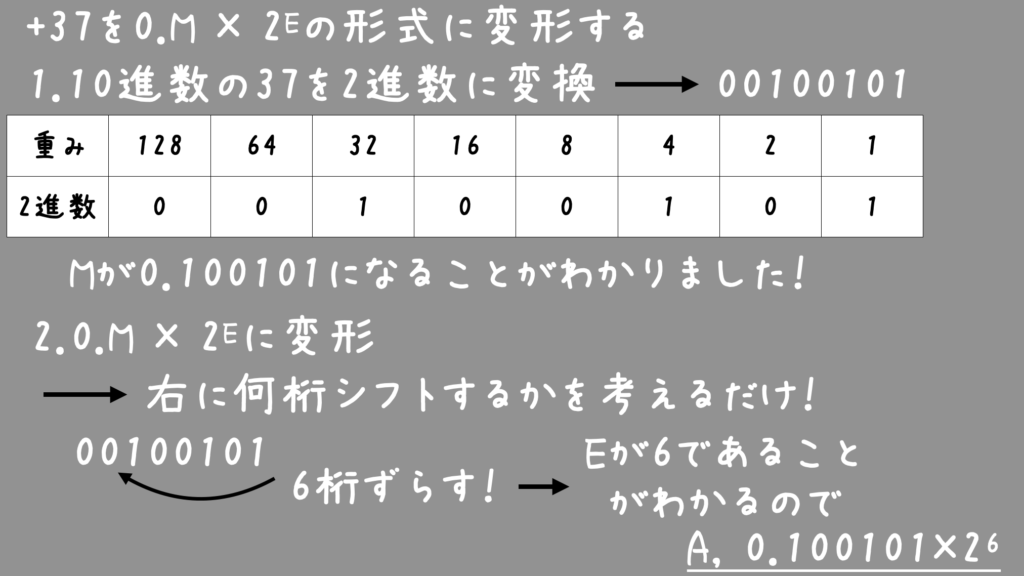
浮動小数点表示の正規化ってなに?

浮動小数点表示の仮数を有効に利用するためのそうさのことを正規化と言います。

平たくいうと、仮数の左側に0が来ないようにするものです。

IEEE形式の浮動小数点表示ってなに？

基本情報技術者試験の午後の試験ではしばしばIEEEが規格化したIEEE形式の浮動小数点表示を使った問題が出題されます。

先の (-1)^s×0.M×2^E この形式とどの様な違いがあるのか説明していきます。

IEEE形式の浮動小数点表示の形式は (-1)^S ×　1.M × 2^E-127 と表す形式です

先ほどまでのIBM形式との違いは仮数が0.Mではなく1.Mとなっている点と、指数が単なるEではなくE-127となっている点です。

(例題)32ビットの2進数である下記はIEEE形式で表された浮動小数点は、10進数でいくらでしょうか。

1.符号Sが1なので負数だとわかります。
2.仮数に1を加えると2進数の1.01です。
3. 1.01を10進数に直すと1.25なのがわかります。
4.指数が10000110なので 128+4+2=134
5.IEEE形式の浮動小数点なので本来の指数は134-127=7
6.-1.25×2⁷だとがわかります。

-1.25×2⁷=-160

まとめ

今回は基数で表現する浮動小数点表示についてまとめていきました。

多少数学的な表現が多かったので難しく感じた人もいるかも知れませんね。

基本情報技術者試験を合格したい方は (-1)^s×0.M×2^E や (-1)^S × 1.M × 2^E-127 の公式に関しては暗記して覚えましょう。