この記事で解決できる内容
※タップすると該当箇所までジャンプできます。
基本情報技術者試験では、データ構造の知識を問う問題が頻出します。スタック、キュー、リスト、配列、木構造などの中でも、木構造はデータ探索の際に重要な知識です。
木構造はデータに上下関係を持たせ、親を上、子を下とする階層的な構造で、特に覚えておきたいのが「2分探索木」です。2分探索木では、親ノードに対し子ノードが最大2つまであり、効率的なデータ検索を可能にします。
ただし、言葉だけでは理解が難しいため、この記事では木構造と2分探索木を図解付きでわかりやすく解説します。
また、過去問にも挑戦しているので、この記事を読むことで試験合格に一歩近づくでしょう。
データ構造の木構造とは
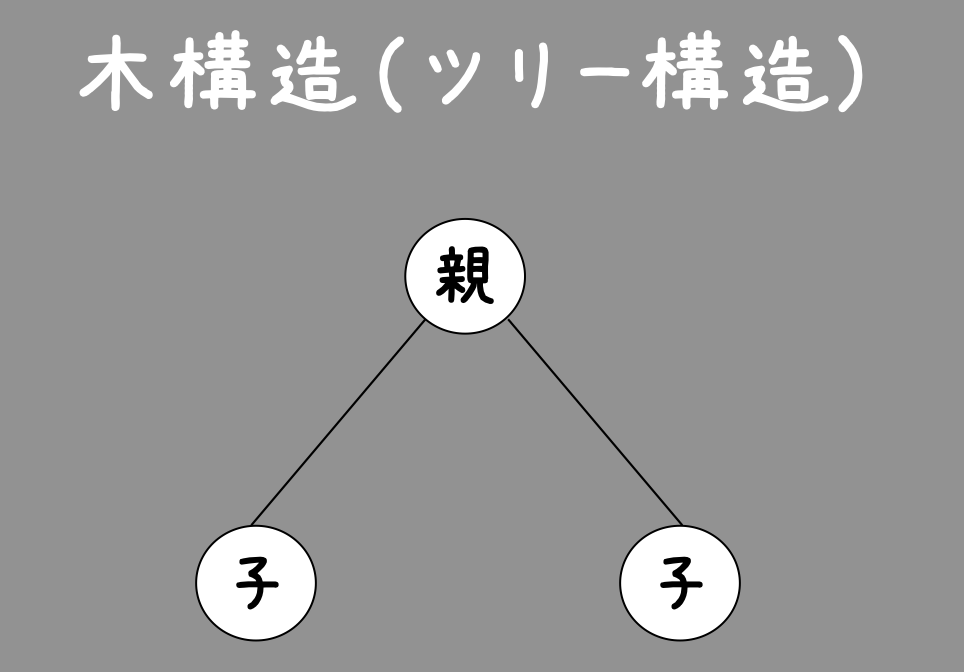
木構造(ツリー構造)とはデータ上に上下関係がある構造で、上を親と呼び、下にあるデータを子と呼びます。子は複数持っているが、どの子も親が一つしか持たない構造になっているものを木構造と呼びます。
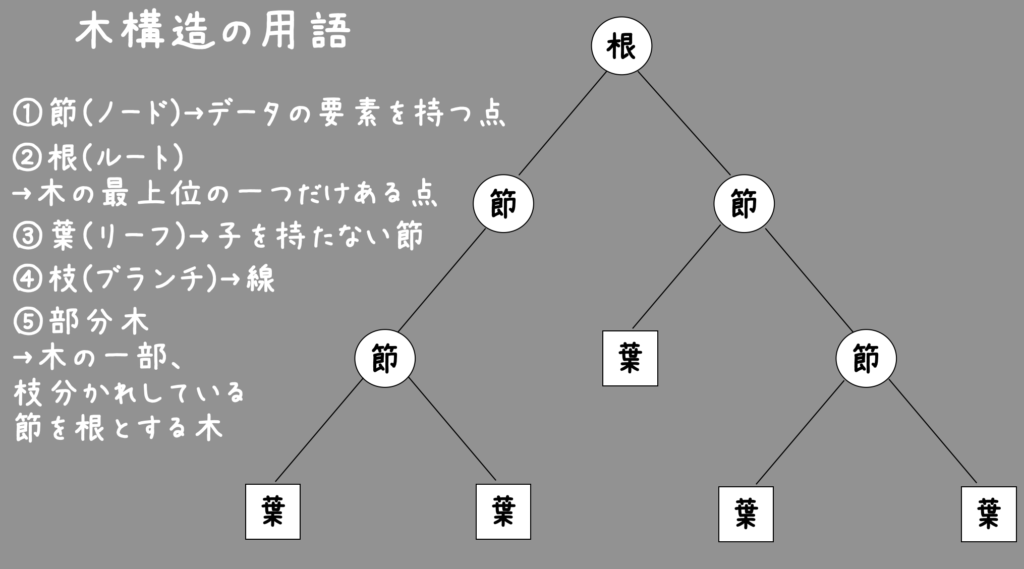
この木構造にはそれぞれ決まった用語があります。
まず一番上にある、親を持たない点を根(ルート)と呼びます。
そしてそれ以外の点を節(ノード)と呼びます。
そして子を持たない一番下っ端の点を葉(リーフ)と呼びます。
そしてその点を結ぶ線を枝(ブランチ)と呼びます。
そしてその一部分を切り取り、ひとつの節を根としてみなすときを部分木と呼びます。
2分木とは
最大二つに分かれる木構造のことを2分木と呼びます。
そして、全ての節がしっかり2つの子を持つ2分木で、葉が同じ段階になるものを完全2分木と呼びます。
ただし、最下位の節は左から順番に埋まっていればみぎの節がなくても完全2分木と呼びます。
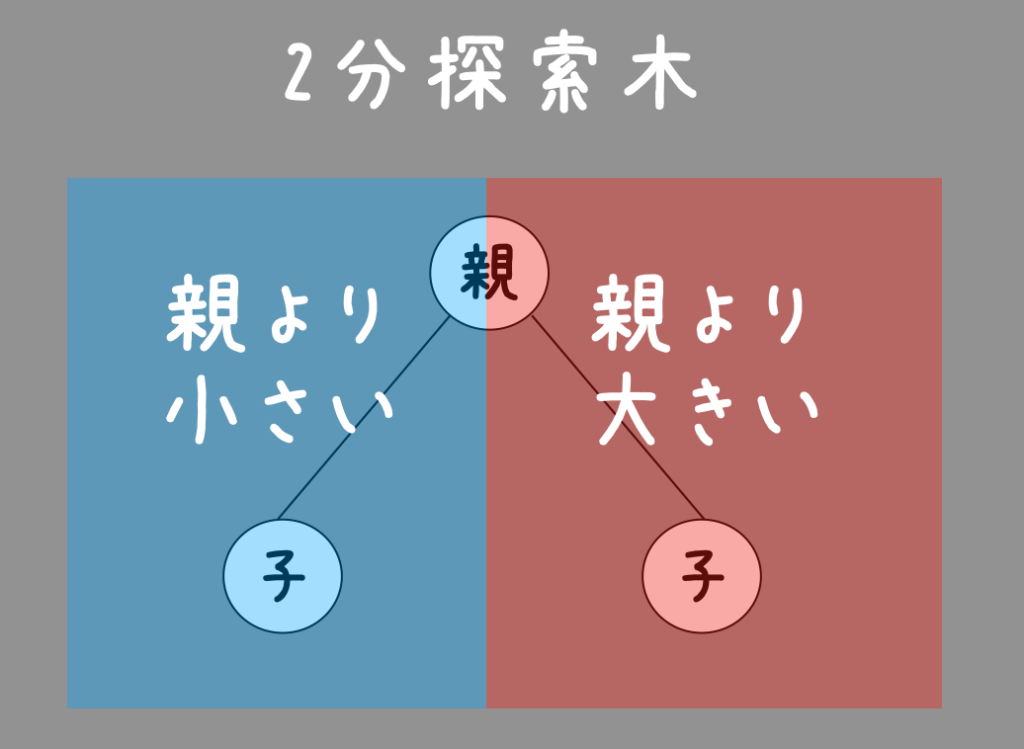
2分探索木とは
規則的に作られたものを2分探索木と呼びます。
その規則とは親の値よりも左の子の値が小さく、右の子の値の方が大きい2分木で構成された構造のこと。
2分探索木に関する過去問題にチャレンジ
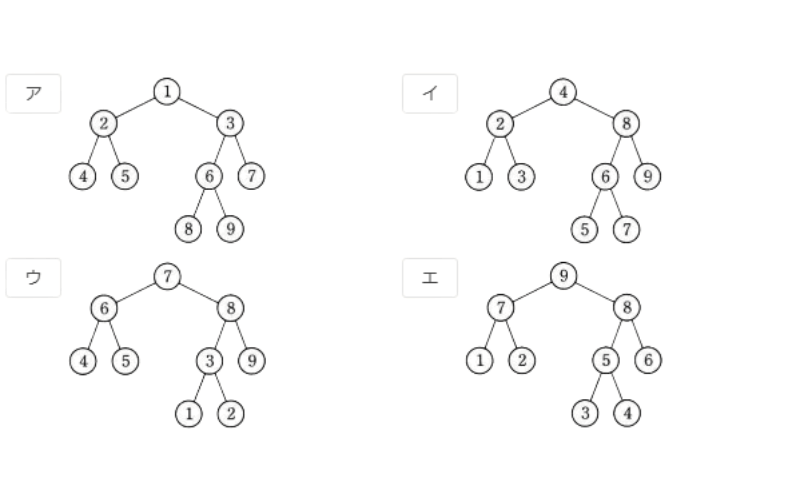
2分探索木として適切なものはどれか。ここで,1~9の数字は,各ノード(節)の値を表す。
出典:平成31年 春期 基本情報技術者試験 問5
さてこの問題を解くのにあたってはまず「2分探索木」とはなにかがわかっていないと解けない問題となっています。
「2分探索木」とは親の左下の子が親よりも小さい値で、親の右下の子の値が親よりも大きい値になっているもののことです。
つまりそうなっているものを選ぶだけの単純な問題だとがわかります。
まずはアを見てみます。
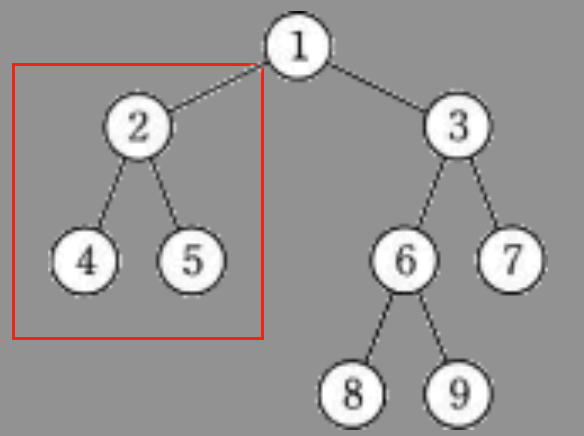
②の左下が2分探索木なら左下は親よりも小さい値でなくてはならないのに、大きくなっています。
よってアは2分探索木ではありません。
続いてイ。
これは全てルールに従っているので2分探索木です。
答えはイ。
一応ウとエもみてみると
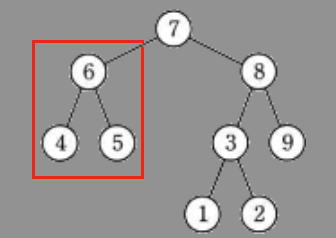
ウ
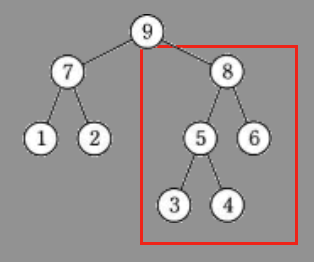
エ
まずはウ。
6の右下の子は本来は6より大きくなければ2分探索木とは呼べないのでNG
そしてエ。
8の右下も8より小さいし、5の右下の子も5より小さい。全然2分探索木じゃない。
よって答えはイで決定。
まとめ
はい、今回は「データ構造の木構造」「2分探索木」についてまとめていきました。
今回の過去問に関しては午前問題なので単純に2分探索木はどれかを問う問題でしたが、追々午後問題では木構造や2分探索木の構造について理解していないと解けないような問題も解説していきますのでしっかり構造を理解しておきましょう。
基本情報技術者試験の合格は独学でも十分可能です!是非他の記事も読んでみてください!
データ構造の基礎知識に関するまとめ
- 木構造とは上下関係のあるデータ構造
- 上を親、下を子と呼ぶ!
- 2分木とは2つの子を持つ木構造
- 2分探索木とは親の左下の子は親よりも小さい値、親の右下の子は親よりも大きい値
全てがこのルールを守っている構造

